8. Ablakolt Fourier-transzformációs módszer, WFTMethod¶
Ezt az eljárást szimulált interferogramon mutatom be. Példaként generálok egyet:
[1]:
import numpy as np
import matplotlib.pyplot as plt
import pysprint as ps
[2]:
g = ps.Generator(1, 4, 2.5, delay=900, GDD=400, FOD=40000, pulse_width=3, resolution=0.05)
g.generate()
mywft = ps.WFTMethod(*g.data)
mywft.plot()
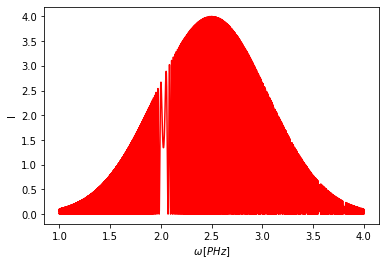
Ablakfüggvény sorozatot adok hozzá az interferogramhoz:
[3]:
mywft.add_window_linspace(2.2, 3.1, 1000, fwhm=0.04, order=2)
FONTOS!
Ha a fenti add_window_linspace lefutott, akkor az ablakfüggvény sorozat már hozzáadódott az interferogramhoz. Ha később megváltoztatnánk bármelyik paraméterét (pl. inkább más fwhm-ot szeretnénk beállítani), akkor az előző ablakfüggvények is megmaradak. Emiatt ajánlott a fenti cellát a következőképpen használni:
[4]:
# az összes hozzáadott ablakfüggvény eltávolítása függetlenül attól, hogy korábban voltak-e
mywft.remove_all_windows()
# ezután adom hozzá az ablakfüggvény sorozatot
mywft.add_window_linspace(2.2, 3.1, 1000, fwhm=0.05, order=2)
Az aktuálisan hozzáadott ablakfüggvényeket a WFTMethod.windows paraméterrel érjük el, ami egy dictionary-t ad vissza, amelyben a key az ablakfüggvény központi helye, a hozzá tartozó value pedig maga az ablakfüggvény reprezentációja (ps.core.window.GaussianWindow). Az interferogram teljes tartományát a cover(N, **kwargs) függvénnyel gyorsabban is elvégezhetjük.
[5]:
len(mywft.windows)
[5]:
1000
Ablakfüggvényt törölni a remove_window_at(center) függvénnyel lehetséges. Ennek az ablakfüggvény központi helyét kell megadni. Ha nincs olyan ablakfüggvény, akkor a hibaüzenetben segítséget nyújt: kiiírja a legközelebbi ablakfüggvényt. Ablakfüggvény intervallum törléséhez a remove_window_interval(start, stop) függvény használható.
[6]:
mywft.remove_window_at(2.25)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-6-09040b9a91a3> in <module>
----> 1 mywft.remove_window_at(2.25)
c:\pyt\pysprint\pysprint\utils\decorators.py in wrapper(self, *args, **kwds)
79 inplace = kwds.pop("inplace", True)
80 if inplace:
---> 81 method(self, *args, **kwds)
82 else:
83 new_ds = method(copy(self), *args, **kwds)
c:\pyt\pysprint\pysprint\core\methods\wft.py in remove_window_at(self, center)
229 )
230 raise ValueError(
--> 231 f"There is no window with center {center}. "
232 f"Did you mean {c[0]}?"
233 )
ValueError: There is no window with center 2.25. Did you mean 2.24954954954955?
Mivel ez a módszer ún. *embarrassingly parallel* számítás, ezért lehetőség van több szálon futtatni a kiértékelést. Ehhez a *Dask* csomagnak telepítve kell lennie (Anaconda-ban alapértelmezetten benne van). Ezt a parallel argumentummal szabályozhatjuk. A többszálas futás általában 50-70% gyorsulást eredményez a single-core módhoz képest. A kiértékelést most parallel=True módon fogom futtatni:
[10]:
mywft.calculate(reference_point=2.5, order=4, fastmath=False, parallel=True);
[########################################] | 100% Completed | 9.2s
Skipped: 0
A fenti calculate függvény ha már egyszer lefutott és megpróbáljuk újra lefuttatni más referencia ponttal vagy más illesztési renddel, akkor a gyorsítótárazás miatt azok már azonnal végrehajtódnak (csak az illesztést számolja újra).
[11]:
mywft.heatmap()
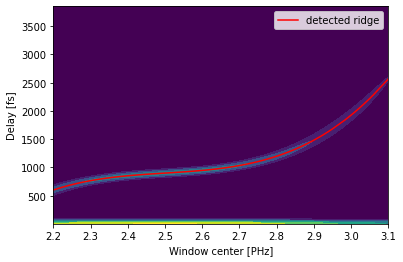
[12]:
mywft.errorplot(percent=True)
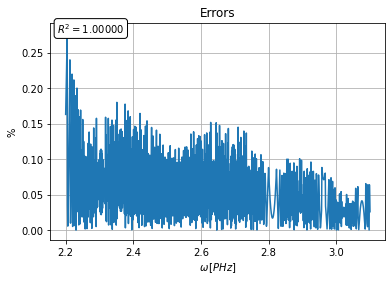
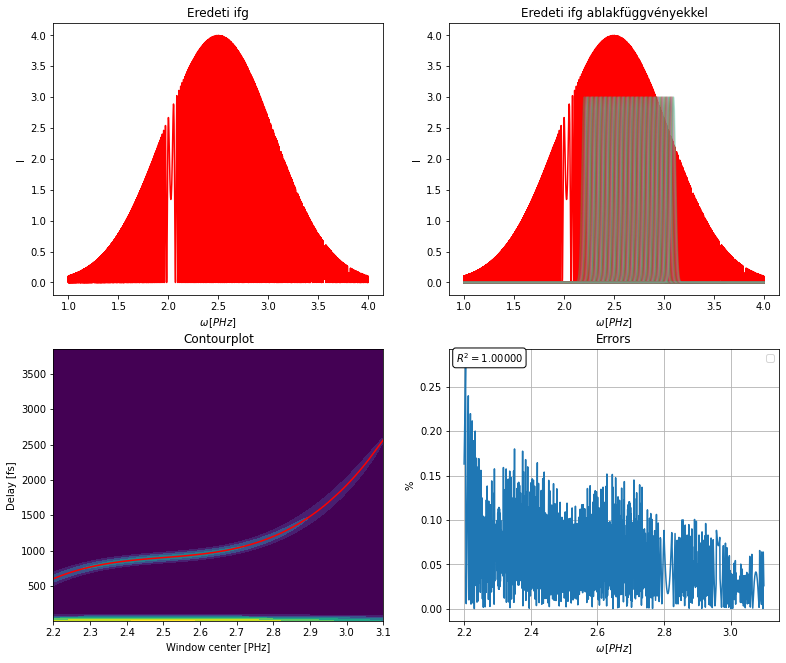
Példa tetszőleges plotok készítésére:
[13]:
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(13, 11))
mywft.plot(ax=ax1)
ax1.set(title="Eredeti ifg")
mywft.view_windows(ax=ax2, maxsize=200, alpha=0.3)
ax2.set(title="Eredeti ifg ablakfüggvényekkel")
mywft.heatmap(ax=ax3, include_ridge=True)
ax3.set(title="Contourplot");
mywft.errorplot(ax=ax4, percent=True)
c:\pyt\pysprint\pysprint\core\methods\wft.py:181: PySprintWarning: Image seems crowded, displaying only a subsample of the given windows.
PySprintWarning
[ legend.py:1193 - _parse_legend_args() ] No handles with labels found to put in legend.
Egy másik szimulált interferogram kiértékelését most parallel=False módon fogom elvégezni, és csak a build_GD függvényt használom, amivel a GD görbét kapom vissza (ps.core.phase.Phase).
[14]:
f = ps.Generator(1, 4, 2.5, delay=1900, GDD=-600, TOD=4000, pulse_width=3, resolution=0.05)
f.generate()
mywft2 = ps.WFTMethod(*f.data)
[15]:
mywft2.add_window_arange(1.5, 3.5, 0.01, std=0.04)
[16]:
GD_gorbe = mywft2.build_GD()
Progress : [==============================] 100% (Skipped: 0)
[17]:
GD_gorbe.plot()
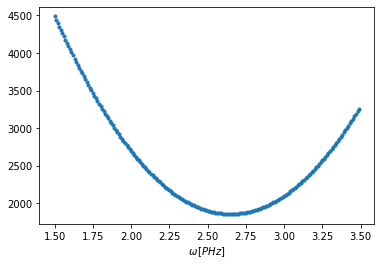
[18]:
GD_gorbe.fit(reference_point=2.5, order=3);
[19]:
GD_gorbe.errorplot(percent=True)
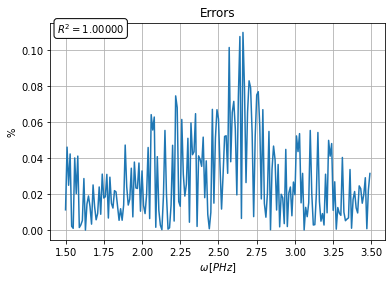
A fastmath opciót itt nem adtam meg. Ez alapértelmezetten True, ilyenkor a heatmap nem hívható, mivel ekkor az ahhoz szükséges adatokat nem építi fel a program.
[20]:
mywft2.heatmap()
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-20-a73a1c58c8ce> in <module>
----> 1 mywft2.heatmap()
c:\pyt\pysprint\pysprint\core\methods\wft.py in heatmap(self, ax, levels, cmap, include_ridge)
587 if self.fastmath:
588 raise ValueError(
--> 589 "You need to recalculate with `fastmath=False` to plot the heatmap."
590 )
591 # Only construct if we need to..
ValueError: You need to recalculate with `fastmath=False` to plot the heatmap.
Néhány hiányosság:
- A gerincvonalat a program automatikusan keresi meg, jelenleg még nincs lehetőség manuálisan állítani. Ez jól működik szimulált példákon, viszont rosszul is teljesíthet valós mérések esetén. Jelenleg ez a része a programnak fejlesztés alatt van (manuális állítás, különböző filterezése a detektált gerincvonalnak, pl. moving avarage validation.)
- Csak egyetlen egy gerincvonalat keres meg, így nem alkalmas pl. kettősen törő optikai szálak esetén, amikor mindkét polarizációs tengelye mentén terjedő módus egyidejűleg gerjesztve van. Szintén fejlesztés alatt van.
8.1 Saját ablakfüggvény használata¶
A program alapbeállításként Gauss ablakfüggvényeket használ, azonban néhány módosítással akár tetszőleges ablakfüggvényt is használhatunk. Tekintsünk most egy Mexican hat waveletet (vagy Ricker waveletet). Ez a következő alakú:
\(A \cdot (1 - (\frac{x-x_0}{a})^2) \cdot e^{-0.5\cdot(\frac{x-x_0}{a})^2}\), ahol \(A = \frac{2}{\sqrt{3a}\cdot\pi^{0.25}}\)
A továbbiakban ezt a waveletet fogjuk példaként használni. Az első lépés a szükséges eszközök importálása. Itt két dologra van szükségünk, a numpy a numerikus rutinokra, illetve a WindowBase osztályra, amely a pysprint.core.window útvonalon érhető el.
import numpy as np
from pysprint.core.window import WindowBase
Minden ablakfüggvényt a WindowBase alosztályaként kell definiálni. Az __init__ szignatúrájában két kötelező argumentum van: x és center. Az x az adott interferogram x tengelyéből kerül a számítás közben megállításra. A center egy egyedi azonosítója az adott ablakfüggvénynek (pl. Gauss függvényeknél a maximum helye, a fenti waveletnél ezt \(x_0\)-val jelöltük). Minden osztály első argumentuma self, ezután definiáljuk a kötelező argumentumokat. Eddig ez így fest:
import numpy as np
from pysprint.core.window import WindowBase
class MexicanHat(WindowBase):
def __init__(self, x, center):
A wavelethez azonban kell egy másik paraméter is, ez az a. Minden használt paramétert meg kell adnunk az __init__ metódusnak, így ezt is adjuk meg. A self kivételével az összes argumentumot az osztályhoz kell “kötni”, hogy a további metódusokban is elérhetőek maradjanak. Tegyük meg:
import numpy as np
from pysprint.core.window import WindowBase
class MexicanHat(WindowBase):
def __init__(self, x, center, a):
# a megadott paraméterek összekötése az osztállyal
self.x = x
self.center = center
self.a = a
Természetesen alapértékeket is adhatuk az általunk használt paramétereknek (itt csak az a-nak), így számítás közben azokat használja majd a szoftver. Esetünkben az A paraméter az a paraméterből számított, így arra az __init__ metódusban nincs szükségünk. Megjegyzés: Az __init__ metódusban ne végezzük számolást, csak a paraméterek inicializálását. Bár ez nem szigorú szabály, mégis a számolásokat a legtöbbször meggyorsítja.
A következő lépés, hogy definiáljuk hogyan számolhatóak ki az ablakfüggvény értékei. Ez egy ún. property lesz, amihez a decorator szintaxist használjuk. Ne aggódjunk, ennek megértése nem fontos és nem szükséges, tekintsünk rá úgy, mint recept. A megfelelő függvényt mindig nevezzük y-nak, amely egyetlen argumentumot fogad el, a self-et. A függvény testébe a matematikai formulákat és egyéb logikát írjuk, ami megmondja hogyan számoljuk ki az ablakfüggvény értékeit. Emlékezzünk vissza,
az __init__-ben megadott paramétereket elérhetjük itt is! A fenti wavelet formuláját beírva kapjuk:
@property
def y(self):
# kiszámoljuk A-t
A = 2 / (np.sqrt(3 * self.a) * (np.pi ** 0.25))
# kiszámítjuk a formulából az értékeket
ys = A * (1 - ((self.x - self.center) / self.a) ** 2) * np.exp(-0.5 * ((self.x - self.center) / self.a) ** 2)
# visszaadjuk a kiszámított értékeket
return ys
Összerakva az egészet:
[21]:
import numpy as np
from pysprint.core.window import WindowBase
class MexicanHat(WindowBase):
def __init__(self, x, center, a):
self.x = x
self.center = center
self.a = a
@property
def y(self):
A = 2 / (np.sqrt(3 * self.a) * (np.pi ** 0.25))
ys = A * (1 - ((self.x - self.center) / self.a) ** 2) * np.exp(-0.5 * ((self.x - self.center) / self.a) ** 2)
return ys
Ezen a ponton minden szükséges részletet megadtunk ahhoz, hogy a program használni tudja a MexicanHat ablakfüggvényt. Előtte azonban ellenőrizzük le, hogy valóban helyes-e a definíció. Minden WindowBase leszármazott osztálynak van plot metódusa. Próbáljuk ki azt!
[22]:
hat = MexicanHat(x=np.linspace(-10, 10, 500), center=0, a=2)
hat.plot()
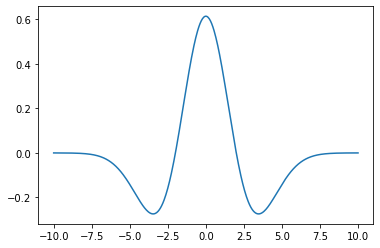
Ez úgy tűnik helyesen adta vissza a kívánt ablakfüggvényt. Használjuk az Ablakot Fourier-transzformációs kiértékeléshez! A korábbiakkal teljesen analóg a számolás menete, egyetlen változtatás, hogy a window_class argumentumnak meg kell adnunk az általunk definiált MexicanHat osztályt.
[23]:
g = ps.Generator(1, 4, 2.5, delay=900, GDD=400, FOD=40000, pulse_width=3, resolution=0.05)
g.generate()
custom_wft = ps.WFTMethod(g.x, g.y, window_class=MexicanHat)
Futtassuk a szokásos lépéseket: adjunk hozzá ablakfüggvény-sorozatot, futtassuk a kiértékelést.
[24]:
custom_wft.add_window_linspace(2.2, 3, 500, a=0.01)
[25]:
custom_wft.calculate(2.5, 4, fastmath=False, parallel=True, ransac=True);
[########################################] | 100% Completed | 5.0s
Skipped: 0
Running RANSAC-filter..
Values dropped: 52 (10.40000 % of total)
[26]:
custom_wft.heatmap()
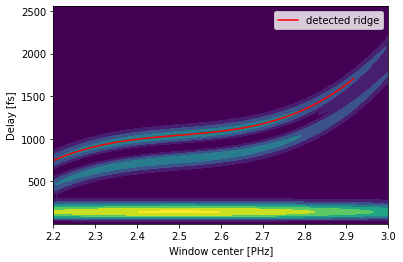
8.2 Egy teljes példa¶
A következőkben egy rossz minőségű interferogramon bemutatom hogyan hozható ki belőle a maximális mennyiségű értékes információ. Töltsük be és vizsgáljuk meg!
[88]:
poor_ifg = ps.WFTMethod.parse_raw('datasets/ifg_poor.trt',
skiprows=8,
decimal=",",
sep=";",
meta_len=6)
poor_ifg.chdomain()
Megjegyzendő, hogy a betöltéssel azonos cellába tettem a tartományváltást, hogy biztosan ne futtassuk le többször az adott interferogramon.
[89]:
poor_ifg.plot()
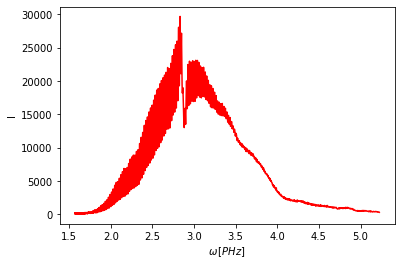
Az első dolgunk, hogy eldöntsük milyen ablakfüggvény-sorozatot állítunk be. Itt egy rövidítést fogok használni, a cover függvényt, amely a teljes tartományt egyenközű módon fogja az ablakfüggvényekket kitölteni.
[90]:
poor_ifg.cover(
N=500, # db ablakfüggvény
fwhm=0.05, # PHz az ablakfüggvény félértékszélessége
order=2, # normál Gauss-függvény
)
Arra számítunk, hogy azonnali futás után nem adódik jó eredmény, a kapott GD görbén még dolgoznunk kell. Ehhez használjuk a build_GD függvényt.
[91]:
gd = poor_ifg.build_GD(fastmath=False, parallel=True)
[########################################] | 100% Completed | 1.0s
Skipped: 85
Vizsgáljuk meg az eredményül kapott csoportkésleltetés görbét:
[92]:
gd.plot()
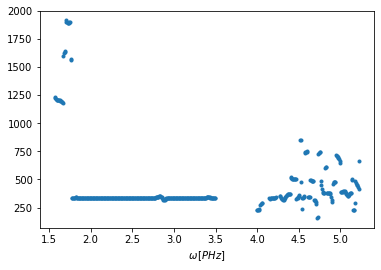
Evidens, hogy a hasznos rész a 1.8 és 3.5 PHz közötti tartomány. Ezt vágjuk ki:
[93]:
gd.slice(1.8, 3.5)
gd.plot()
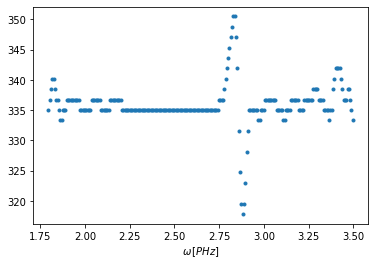
A grafikon alapján rossznak tűnhet a helyzet, de a függőleges koordináta nagyságrendben különbözik az előző ábrától. Ezen a ponton illeszthetnénk is, de van még további mód a javításra. Használjuk az ún. RANSAC szűrést. Az algoritmus leírása túlmutat ezen oldal feladatán, a megadott linken olvashatunk róla. A gd objektumon a ransac_filter függvénnyel, illetve az apply_filter függvénnyel használható. Ugyan elsőrendű függvény
várunk, mégis valamilyen kis nemzéró maradék diszperziója az üres spektrométernek is lehet. Emiatt a szűrést legalább másodrendben kell végeznünk, hogy a valódi zajt távolítsuk el, és ne a spektrométerre jellemző sajátosságokat.
[94]:
gd.ransac_filter(order=2, plot=True, residual_threshold=0.4)
plt.legend();
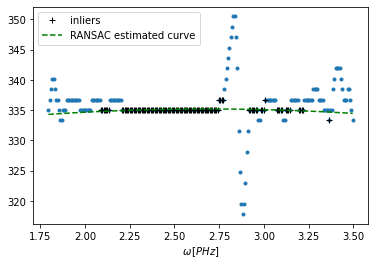
Ezzel intelligens módon kiszűrtük a zaj legnagyobb részét a csoportkésleltetés görbéből. Innen már nincs más dolgunk, mint alkalmazni a szűrőt, majd függvényt illeszteni és kiszámolni az együtthatókat.
[95]:
gd.apply_filter()
Values dropped: 123 (52.78970 % of total)
[96]:
gd.fit(reference_point=2.355, order=3);